Minimize Travel Tax DSA Interview Problem

In Minimize Travel Tax DSA Interview Problem If we could determine the number of trips in which we pay the tax for some node, we can estimate the contribution of the node in the sum. We can do this using the idea of prefix sums on tree. Now that we can reduce the taxes for nodes that are not adjacent, we can use dynamic programming to solve this subproblem and calculate the required answer.

Let’s first the actual problem and then try to solve the problem together

Minimize Travel Tax DSA Interview Problem

There are $n$

$n$ cities connected by $n - 1$

$n-1$ bi-directional roads such that all the cities are connected.

You go on $m$

$m$ trips where on the $i - t h$

$i-th$ trip you travel from city $u_{i}$

$u_i$ to city $v_{i}$

$v_i$ . All the trips are independent of each other. You have to pay a tax of $t a x_{i}$

$tax_i$ on entering or leaving the $i - t h$

$i-th$ city. If you pay the tax while entering then you don’t need to pay at the time of leaving.

You can choose some non-adjacent cities and make their tax half. What can be the minimum sum of taxes you pay for all the $m$

$m$ trips?

Input

The first line contains a single integer $t$

$t$ $(1 \leq t \leq 10^{4})$

$(1 \leq t \leq 10^4)$ — the number of test cases. The description of $t$

$t$ testcase follows.

The first line of each testcase contains two integers $n$

$n$ and $m$

$m$ $(1 \leq n, m \leq 10^{5})$

$(1 \le n,m \le 10^5)$ — the number of nodes and the number of trips. The nodes are numbered $1, 2, \dots, n$

$1,2,…,n$ .

The second line contains $n$

$n$ space separated integers $t a x_{1}, t a x_{2}, . . . t a x_{n}$

$tax_1,tax_2,...tax_n$ $(2 \leq t a x_{i} \leq 10^{9}; t a x_{i} % 2 == 0)$

$(2 \le tax_i \le 10^9; \hspace{2 pt} tax_i\%2 == 0)$ denoting the taxes at the nodes of the tree.

The next $n - 1$

$n-1$ lines describe the tree. Each contains two space separated integers $u$

$u$ and $v$

$v$ $(1 \leq u, v \leq n; u \neq v)$

$(1 \le u, v \le n; u \neq v \hspace{1 pt})$ denoting an edge between vertices $u$

$u$ and $v$

$v$ . It is guaranteed that these edges form a tree.

Finally, there are $m$

$m$ lines describing the trips. Each line contains two integers $u$

$u$ and $v$

$v$ $(1 \leq u, v \leq n; u \neq v)$

$(1 \le u, v \le n; u \neq v \hspace{1 pt})$ denoting a trip from city to $u$

$u$ to city $v$

$v$ .

It is guaranteed that the sum of $n$

$n$ and $m$

$m$ over all test cases does not exceed $10^{5}$

$10^5$ each.

Output

For each testcase, print a single integer — the minimum sum of taxes you pay for all the trips in a single line.

Example

Input

Output

13
10

Note

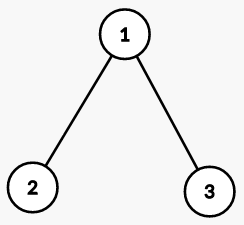$9fe07161561d664131c842fc3525449dcf4e3c5f$ Sample test case 1In sample testcase 1,

For trip 1, from 1 to 3: you will have to pay taxes at cities 1 and 3.
For trip 2, from 3 to 2: you will have to pay taxes at cities 1,2 and 3.

You can reduce the taxes at cities 2 and 3. Then the net tax will be $2 \times 2 + 1 \times 1 + 4 \times 2 = 13$

$2\times2+1 \times 1+4\times2=13$ .So,the ans is $13$

$13$ .

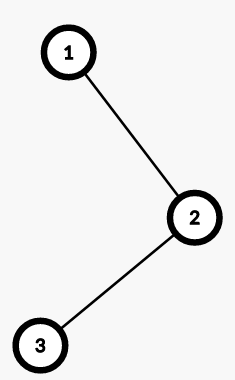$4698838d0ff9814a247900df3b887243b7ca8a04$ Sample test case 2In sample testcase 2,

For trip 1, from 1 to 3: you will have to pay taxes at cities 1, 2 and 3.
For trip 2, from 1 to 2: you will have to pay taxes at cities 1 and 2.

You can reduce the taxes at city 2. Then the net tax udll be $2 \times 2 + 2 \times 2 + 2 \times 1 = 10$

$2\times2+2\times2+2\times1=10$ . So,the ans is $10$

$10$ .

Minimize Travel Tax Solution in C++

#include <bits/stdc++.h>
using namespace std;

void dfs(long long src,long long dis,long long p,vector<long long> adj[],vector<vector<long long>> &dp,vector<long long> &h)
{
h[src]=dis;
for(auto x: adj[src])
{
if(x!=p)
{
dp[x][0]=src;
dfs(x,dis+1,src,adj,dp,h);
}
}
}
long long kanc(long long x,long long k,vector<vector<long long>> &dp)
{
long long step=0;
long long node=x;
while(k!=0)
{
if(k%2)
{
node=dp[node][step];
if(node==0)
return 0;
}
k/=2;
step++;
}
return node;
}
long long lca(long long n1,long long n2,vector<long long> &h,vector<vector<long long>> &dp)
{
long long diff=abs(h[n1]-h[n2]);
if(h[n1]>h[n2])
{
n1=kanc(n1,diff,dp);
}
else
{
n2=kanc(n2,diff,dp);
}

if(n1==n2)
return n1;

long long jump=h[n1];
while(jump!=0)
{
long long v1=kanc(n1,jump,dp);
long long v2=kanc(n2,jump,dp);
if(v1==v2)
jump/=2;
else
{
n1=v1;
n2=v2;
}
}
return dp[n1][0];
}
long long dfs2(long long src,long long p,vector<long long> adj[],vector<long long> &times)
{
for(auto x:adj[src])
{
if(x!=p)
{
times[src]+=dfs2(x,src,adj,times);
}
}
return times[src];
}
long long cost(long long src,long long p,vector<long long> adj[],long long reduce,vector<long long> &tax,vector<vector<long long>> &d)
{
if(d[src][reduce]!=-1)
return d[src][reduce];

long long ans;
if(reduce)
{
ans=tax[src]/2;
}
else
{
ans=tax[src];
}
for(auto x: adj[src])
{
if(x!=p)
{
if(reduce)
ans+=cost(x,src,adj,0,tax,d);
else
ans+=min(cost(x,src,adj,0,tax,d),cost(x,src,adj,1,tax,d));
}
}
return d[src][reduce]=ans;
}
int main() {

long long t;
cin>>t;
while(t--)
{
long long n,m;
cin>>n>>m;

vector<long long> tax(n+1);
for(long long i=1;i<=n;i++)
cin>>tax[i];

vector<long long> adj[n+1];
for(long long i=1;i<n;i++)
{
long long u,v;
cin>>u>>v;

adj[u].push_back(v);
adj[v].push_back(u);
}

vector<vector<long long>> dp(n+1,vector<long long>(18,0));
vector<long long> h(n+1);

dfs(1,0,0,adj,dp,h);

for(long long j=1;j<=17;j++)
{
for(long long i=1;i<=n;i++)
dp[i][j]=dp[dp[i][j-1]][j-1];
}

vector<long long> times(n+1,0);
while(m--)
{
long long x,y;
cin>>x>>y;

long long z=lca(x,y,h,dp);

times[x]+=1;
times[y]+=1;
times[z]-=1;
times[dp[z][0]]-=1;
}
dfs2(1,0,adj,times);

for(long long i=1;i<=n;i++)
tax[i]*=times[i];

vector<vector<long long>> d(n+1,vector<long long>(2,-1));
cout<<min(cost(1,0,adj,0,tax,d),cost(1,0,adj,1,tax,d))<<endl;
}
return 0;

}

Minimize Travel Tax DSA Interview Problem

Minimize Travel Tax DSA Interview Problem

Minimize Travel Tax Solution in C++

1 thought on “Minimize Travel Tax DSA Interview Problem”

Leave a Comment Cancel reply