Expected Path Length III DSA Interview Problem

Posted by admin July 12, 2023
Expected Path Length III DSA Interview Problem
Expected Path Length III DSA Interview Problem

Expected Path Length III DSA Interview Problem involves Numbers theory, Probability and Exception and Dynamic Programming concepts. Let’s first see the actual problem and then solve it together:

 Expected Path Length III DSA Interview Problem Statement

You choose a natural number from 1 to

n (each number being equally likely) and do the following procedure:

  • Initialize a variable
    step=0     

    .

  • Let
    X     

    be the current number you have.

  • Randomly choose any divisor of
    X     

    (each divisor being equally likely). Let it be

    Y 

    , now replace

    X 

    by

    X/Y 

    . Also, increment step by

    1 

    .

  • If
    X     

    is not equal to

    1 

    , repeat from

    2nd 

    step.Let expected value of step be represented in the form of a irreducible fraction

    x/y. Return

    xy−1 mod

    (109+7), where

    y−1 is the modulo multiplicative inverse of

    y modulo

    (109+7).

Input

The first and only line of input contains an integer

n

(1≤n≤105).

Output

Print a single integer — the expected value of step modulo

109+7.

Examples
Input
1
Output
0
Input
2
Output
1
Note

In sample testcase

1, The only possible

X we can choose is

1.

For

X=1,step=0. Therefore,expected path length = 0.

In sample testcase

2, Different possible sequences of steps are:

{[1],[2,1],[2,2,1],[2,2,2,1],...}

with their corresponding value of step as:

0,1,2,3,..... It is found that the expected value is

1.

Expected Path Length III DSA Interview Problem Solution:

Let E(x) denote the expected value of step for a given value of x. Also let k denote the number of divisors of x. We can work out the following expression for E(x) using the definition of E(x)

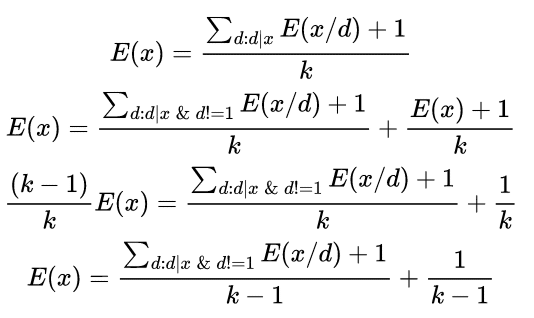
We can now use math and dynamic programming to calculate E(x) through this expression.

Approach

Calculating divisors using Harmonic LemmaOne of the subproblems is to calculate the divisors for each x from 1 to A. We can do the same using the following code

vector<vector<int>> divisors(A+1);
for(int i=2; i<=A; i++){
for(int mul=i; mul<=A; mul+=i){
divisors[mul].push_back(i);
}
}

The number of operations performed in the above code can be given as A/1 + A/2 + … A/A which is bounded by O(AlogA).

Using Fermat’s Little Theorem and Binary exponentiation to calculate Multiplicative Modular Inverse

Please refer this article to learn to calculate modular inverse using Binary exponentiation.

Solving for a given x using Dynamic programming

Let dp[i] denote the expected value of step for a given i. Now we can use the expression derived earlier to calculate E(x) by dynamic programming as follows:

vector<int> dp(A+1,0);
for(int i=2; i<=A; i++){
dp[i] = (0LL + dp[i] + (1LL*(1)*expm(divisors[i].size(),mod-2))%mod)%mod;
for(int d:divisors[i]){
dp[i] = (0LL + dp[i] + (1LL*(dp[i/d]+1)*expm(divisors[i].size(),mod-2))%mod)%mod;
}
}

Note that we dont add 1 in the list of divisors hence we dont need to subtract 1 from k in the denominator.

Calculating the final answer

Since each number is chosen randomly and equiprobable the final answer can be obtained by summing the value of E(x) for each x from 1 to A and then multiplying by 1/A (that is by the multiplicative inverse of A modulo the given prime).

int ans = 0;
for(int i=1; i<=A; i++) ans = (ans + dp[i])%mod;
ans = (1LL*ans * expm(A,mod-2))%mod;We have thus solved the problem in a complexity of O(AlogA)

Ok Let’s see the final solution.

Expected Path Length III DSA Interview Problem Solution

#include<bits/stdc++.h>
using namespace std;


long long binaryexp( long long a , long long b , long long mod ){
long long res = 1;
while(b){
if(b&1){
res = (res*a)%mod;
}
a=(a*a)%mod;
b>>=1;
}
return res;
}


long long invmod(long long a, long long mod ){
return binaryexp(a,mod-2,mod)%mod;
}




int main(){
long long mod = 1e9+7;
int n; cin>>n;
long long dp[n+1] , cnt[n+1];
for( int i = 2 ; i<n+1 ; i++ ){
dp[i]=1;
cnt[i]=1; // no. of divisors
}
dp[1]=0;
for( int i = 2 ; i <= n ; i++ ){
cnt[i]++; dp[i]=(dp[i]+1)%mod;
dp[i]=(dp[i]%mod*invmod(cnt[i]-1,mod)%mod)%mod;
for( int j = 2*i ; j<=n ; j+=i ){
dp[j]=(dp[j]+1+dp[i])%mod;
cnt[j]++;
}
}
long long ans = 0;
for( int i = 1 ; i <= n ; i++ ) ans = (ans+dp[i])%mod;
ans = (ans%mod*invmod(n,mod)%mod)%mod;
cout<<ans;
}